Matemático do Mês 1

       Como professora de Matemática A do 12º ano, no início do ano letivo, propus aos meus alunos uma atividade de enriquecimento extracurricular. Esta consiste em encontrar Matemáticos que tivessem nascido ou falecido no mês corrente, recolhendo algumas curiosidades da sua vida e o modo como contribuíram para esta área científica. 
     Aliado ao facto de que existem ou existiram pessoas cujos nomes são muitas vezes desconhecidos, mas que, ao longo dos vários séculos deram o seu contributo para a Matemática, os objetivos desta atividade são incentivar a curiosidade e ampliar os conhecimentos.

     Alguns alunos já deram o seu contributo, sendo os seus trabalhos, resultado de variadas pesquisas, publicados na página da disciplina e comentados nas aulas. Como aderiram com entusiasmo à sugestão da divulgação dos mesmos do Jornal do Agrupamento vamos passar à sua publicação.

Graça Ferreira Carreira

    Gilles Personne de Roberval nasceu a 9 de agosto de 1602, em Roberval, França, e morreu a 27 de outubro de 1675, em Paris, França. Matemático e filósofo foi inventor da balança de Roberval, além de outras contribuições na matemática.

     Esteve na cadeira de matemática no Colégio Real de França. A condição de estar nesta cadeira era que o titular devia propor questões matemáticas para solucionar, e devia renunciar em favor de qualquer pessoa que tivesse resolvido tais questões melhor do que ele. Mas, apesar disso, Roberval foi capaz de manter a cadeira até sua morte.

Roberval foi um dos matemáticos que, pouco antes da invenção do cálculo infinitesimal, ocuparam a atenção dos problemas que só são solucionáveis, ou podem ser resolvidos mais facilmente, por algum método que envolve limites ou infinitesimais, que hoje seria resolvido pelo cálculo. Ele trabalhou na quadratura das superfícies e da cubagem de sólidos, que ele realizou, em alguns dos casos mais simples, através de um método original que ele chamou de "Método dos indivisíveis", mas ele perdeu boa parte do crédito da descoberta, mantendo o seu método para uso próprio.

Outra das descobertas de Roberval era um método bastante geral dos desenhos tangentes, considerando uma curva descrita por um ponto móvel cujo movimento é a resultante de vários movimentos mais simples. Ele também descobriu um método de obter uma curva de outro, por meio do qual as áreas finitas podem ser obtidas iguais para as áreas entre as curvas certas e suas assímptotas.

Artur Fonseca,nº5 do 12ºA

 

       Gottlob Frege nasceu a 8 de novembro de 1848 na  Alemanha. Estudou nas Universidades de Jena (1869-1871) e na Universidade e de Gottingen (1871-1873), dedicando-se à Matemática, à Física e à Química.

     Ensinou na Universidade de Jena no departamento de Matemática onde permaneceu o resto da sua vida profissional. Inicialmente ensinava qualquer ramo da matemática mas as suas publicações eram fundamentalmente no campo da lógica.

    Os seus estudos em Filosofia da Lógica, Filosofia da Matemática e Filosofia da Linguagem fazem de Frege um dos maiores matemáticos, lógicos e filósofos de sempre.

    Frege queria mostrar que a aritmética era idêntica à lógica e pode-se dizer que recriou a disciplina da lógica ao construir o primeiro «cálculo de predicados». Um cálculo de predicados é um sistema formal constituído por duas componentes: a linguagem formal e a lógica.

    Tal como Leibniz (1646-1716),  Frege pensava que a característica específica da Matemática era a construção de cálculos que poderiam ser interpretados sem referência a números ou quantidades.

     Frege foi mais longe do que qualquer dos seus predecessores na sua exigência de rigor formal dentro da lógica, e a teoria dedutiva ou cálculo que elaborou é a maior realização alguma vez alcançada na história da lógica.

    Confrontado com a ambiguidade da linguagem usual e com a inadequação dos sistemas lógicos existentes, Frege inventou inúmeras notações simbólicas, tais como  quantificadores e variáveis, que pudessem fornecer fundamentos para a lógica matemática moderna. No entanto, o seu trabalho não foi muito bem recebido. Aliás, pode mesmo dizer-se que, inicialmente, foi ignorado.

    Frege faleceu a 26 julho de 1925 na Alemanha.

                                                                                             Ruben Pastilha, nº 23, 12ºA

 

Évariste Galois (1811-1832)

"Infelizmente, é pouco reconhecido o facto dos livros científicos mais importantes serem aqueles onde o autor diz com clareza aquilo que não sabe". (Galois).

  Évariste Galois, matemático francês, nasceu em Bourg-la-Reine a 25 de outubro de 1811 e morreu em Paris a 31 de maio de 1832, com apenas 20 anos.

        Foi um dos maiores matemáticos de todos os tempos e um exemplo de um precoce génio matemático. Não só resolveu um dos problemas mais antigos, ao determinar a condição necessária e suficiente para que um polinómio pudesse ser resolvido por raízes, como criou um domínio inteiramente novo da álgebra abstracta: a Teoria dos Grupos.

        Galois cresceu durante um período de grande agitação social e política, colocando-se, frequentemente, no centro de controvérsias, o que não apenas o afastou de sua brilhante carreira, como também acabou por levá-lo a uma morte prematura. Mas, antes de morrer, deixou os seus inéditos manuscritos científicos (Escritos de Galois) ao seu amigo Auguste Chevalier, também matemático, juntamente com uma carta escrita na véspera da sua morte.

        O seu principal trabalho foi sobre a possibilidade de resolução das equações algébricas, mas este não foi considerado digno de atenção pelo grande A. Cauchy e tido por demasiado obscuro por Poisson. Só em 1846, vários anos após a sua morte, foi publicado por J. Liouville, no seu jornal, mas a sua importância só foi compreendida quando C. Jordan consagrou o seu Tratado das Substituições a Equações Algébricas.

        Este havia conseguido expor as condições necessárias e suficientes à resolução das equações algébricas por meio de radicais.

       O seu trabalho só foi  reconhecido uma década após a sua morte, chegando-se à conclusão de que Galois tinha de facto formulado uma completa explicação de como se poderia obter soluções para as equações do quinto grau.

                                                                                                        Diana Ferreira 12ºA

Leonhard Euler nasceu a 15 de abril de 1707, na Suíça, e morreu a 18 de setembro de 1783, na Rússia.
Foi um grande matemático e físico suíço, pois fez importantes descobertas em campos variados. Ele contribuiu de variadas formas para a Matemática no campo da terminologia e notação, em especial para as análises matemáticas, como a noção de uma função.
         Euler é considerado um dos mais “proeminentes matemáticos do século XVIII”, uma declaração feita por Pierre- Simon Laplace, um outro matemático que muito cooperou, sobretudo no campo das probabilidades.
Na Matemática um dos seus contributos foi a chamada fórmula de Euler, esta fórmula matemática mostra a relação entre as funções trigonométricas e a função exponencial. A fórmula é dada por:

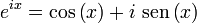
em que :

x é um número real;

                 e é a base do logaritmo natural;    
           

      é um número complexo;

seno e co-seno são funções trigonométricas.

                                            Gabriela Teixeira Carrasqueiro 12ºA

Benoit Mandelbrot

(1924-2010)

Benoit Mandelbrot, matemático francês, nasceu a 20 de novembro de 1924 em Varsóvia, na Polónia e faleceu a 14 de outubro de 2010.

Cedo foi introduzido a conceitos matemáticos e físicos por vários membros da família ligados ao mundo académico.

       A sua mãe foi uma das primeiras médicas licenciadas na Rússia e o seu tio, responsável pela sua educação, era professor de Matemática  no Collège de France em Paris.
     A família Mandelbrot fugiu para França em 1936, três anos após a subida de Hitler ao poder e três anos antes do início da II.ª Guerra Mundial.     

    Benoit frequentou o Lycze Rolin em Paris, depois estudou em Lyon, e, mais tarde, foi para os EUA. Por fim estudou na École Polytechnique e na Sorbonne, em Paris e no Instituto Californiano de Tecnologia. A sua carreira académica dividiu-se principalmente entre França e EUA.
       Este foi o primeiro homem a descrever o mundo da forma como ele é. Antes de Benoit quase toda a geometria que se conhecia era fundada pelo grego Euclides, que era a geometria das linhas, dos pontos, das esferas, dos cones, etc.

      Mandelbrot começou a ficar um pouco insatisfeito em relação à Geometria Clássica, uma vez que, ao explorar e resolver diversos problemas, os pontos, as linhas rectas e os círculos não demonstravam ser abstracções adequadas para compreender a complexidade da natureza.

      Ele deixou bem claro que as irregularidades da natureza são de uma regularidade impressionante, desvendando uma realidade além da imaginação: um lugar onde coisas infinitamente grandes podem caber num espaço pequeno e limitado, uma terra com mais dimensões do que as três que nós conseguimos ver.

      A sua pesquisa forneceu teorias matemáticas para o fenómeno da probabilidade errática e métodos de auto-semelhanças em probabilidades. Pesquisas realizadas sobre processos esporádicos, termodinâmica, geomorfologia, gráficos e arte (com a ajuda do computador) criaram e desenvolveram a geometria fractal.

      Este prodigioso e ilustre matemático contemporâneo é conhecido mundialmente como sendo o único responsável pelo enorme interesse nos chamados objectos fractais. Hoje em dia a sua geometria é conhecida através de bonitas ilustrações coloridas que, enriqueceram tanto a matemática moderna como a arte.

O que é um fractal?

     Um fractal  é um objecto geométrico que pode ser dividido em partes, cada uma das quais semelhantes ao objecto original. Os fractais têm infinitos detalhes, são geralmente autossimilares e não dependem de escala. Em muitos casos um fractal pode ser gerado por um padrão repetido. A geometria fractal foi descoberta em 1970 e o termo fractal foi criado em 1975 a partir do adjectivo latino fractus, que significa quebrar.

 

<><>

Daniela Silva nº12 12ºA